Midterm Surge and Decline: Political Pattern or Statistical Artifact?

The phenomenon of midterm surge and decline has become a staple of American electoral commentary, appearing in nearly every journalistic account of congressional midterm elections. The pattern seems intuitive: the party that wins the presidency typically loses ground in the subsequent midterm election, while the opposition party gains seats. But is this really evidence of meaningful political dynamics, or might we be imposing patterns on what amounts to statistical noise?

The Midterm Surge and Decline Theory

The theory of midterm surge and decline, as articulated by James Campbell (1991), suggests a systematic relationship between presidential election performance and subsequent midterm results. According to Campbell, “In midterm elections, the greater a party’s prior presidential vote margin … the greater its loss of congressional votes and seats” (p. 483). This observation has spawned numerous explanations rooted in voter psychology and political behavior.

Political scientists have proposed several mechanisms to explain this pattern. Some argue that public mood inevitably turns against the president as the honeymoon period fades. Others point to supporter fatigue, suggesting that the party base becomes less energized after achieving victory. Additional theories propose that voters grow wary of the president’s agenda or become disillusioned when campaign promises go unfulfilled. There’s also the possibility that the public develops sympathy for the out-of-power party, viewing them more favorably as the negative associations from their previous time in office fade from memory.

A Statistical Alternative: Regression to the Mean

While these psychological explanations hold intuitive appeal, I want to propose a different perspective: what if midterm decline is simply regression to the mean rather than evidence of meaningful political dynamics? This argument echoes David Mayhew’s (2000) observation that the same number of presidential “runs” explained by critical elections theory can be produced by flipping a coin. Humans have a well-documented tendency to impose patterns and explanations on stochastic processes, and electoral politics may be no exception.

A Downsian model of elections provides a useful starting point for this analysis. Anthony Downs (1957) demonstrated that in two-party competition, parties position themselves to win elections by locating near the median voter’s preferred position. This spatial model predicts that parties will converge toward the center and roughly divide the vote equally. While this greatly simplifies electoral complexity, it does capture an important feature of American presidential politics: as Mayhew (2008) notes, Democrats and Republicans have historically split open seat presidential elections nearly evenly.

Consider a simple simulation where partisan vote shares are normally distributed with a mean of 50 percent and a standard deviation of 5 percent. (The specific value assigned as standard deviation is not particularly important but it helps to illustrate the concept being discussed.) Using this distribution to simulate 500 sets of presidential and midterm elections, we can generate random outcomes for a party in presidential and midterm elections. As shown in Figure 1, these assumptions produce no correlation between presidential and midterm election vote shares.

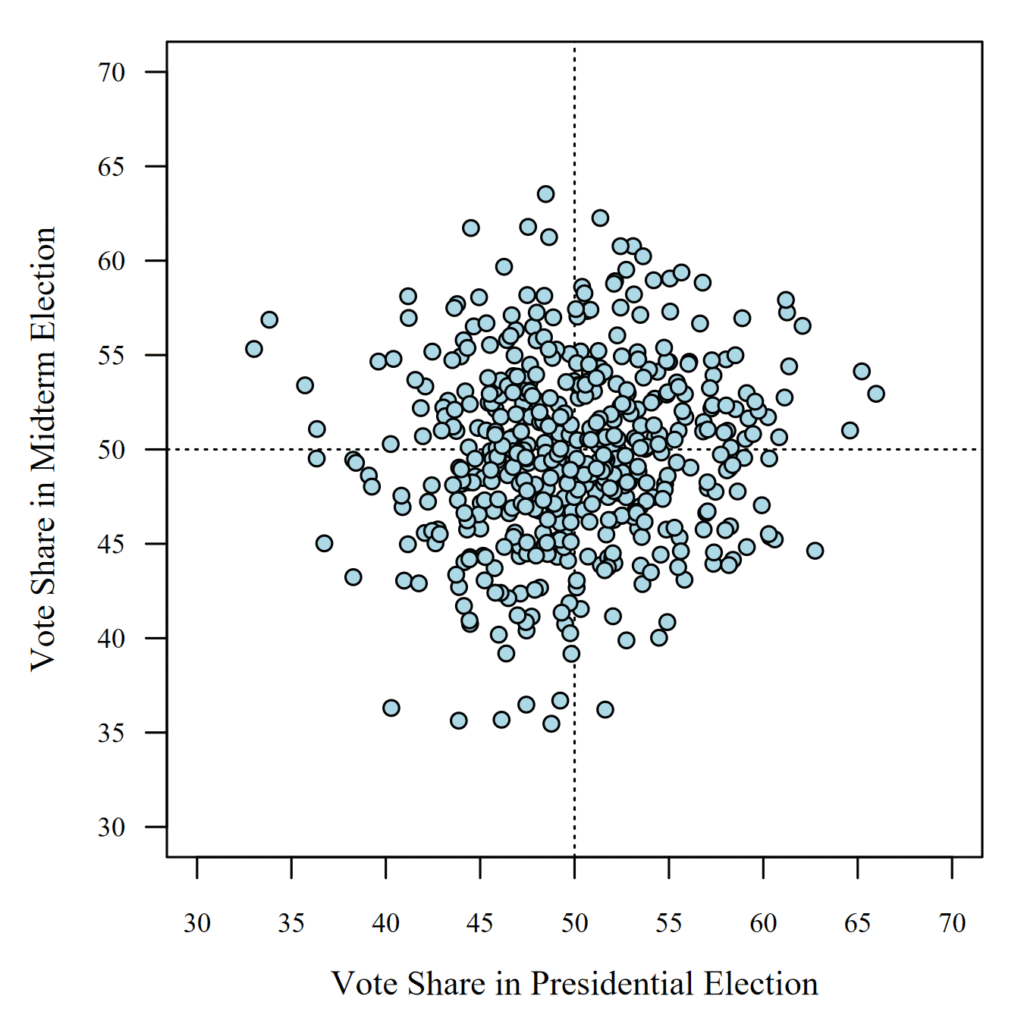
Now consider whether the party gains or loses vote share in the midterm election relative to its performance in the presidential election. In Figure 2, we observe a classic regression to the mean. The greater the party’s margin of victory (or defeat) in the presidential election, the greater its expected decline (or surge) in the subsequent midterm election.

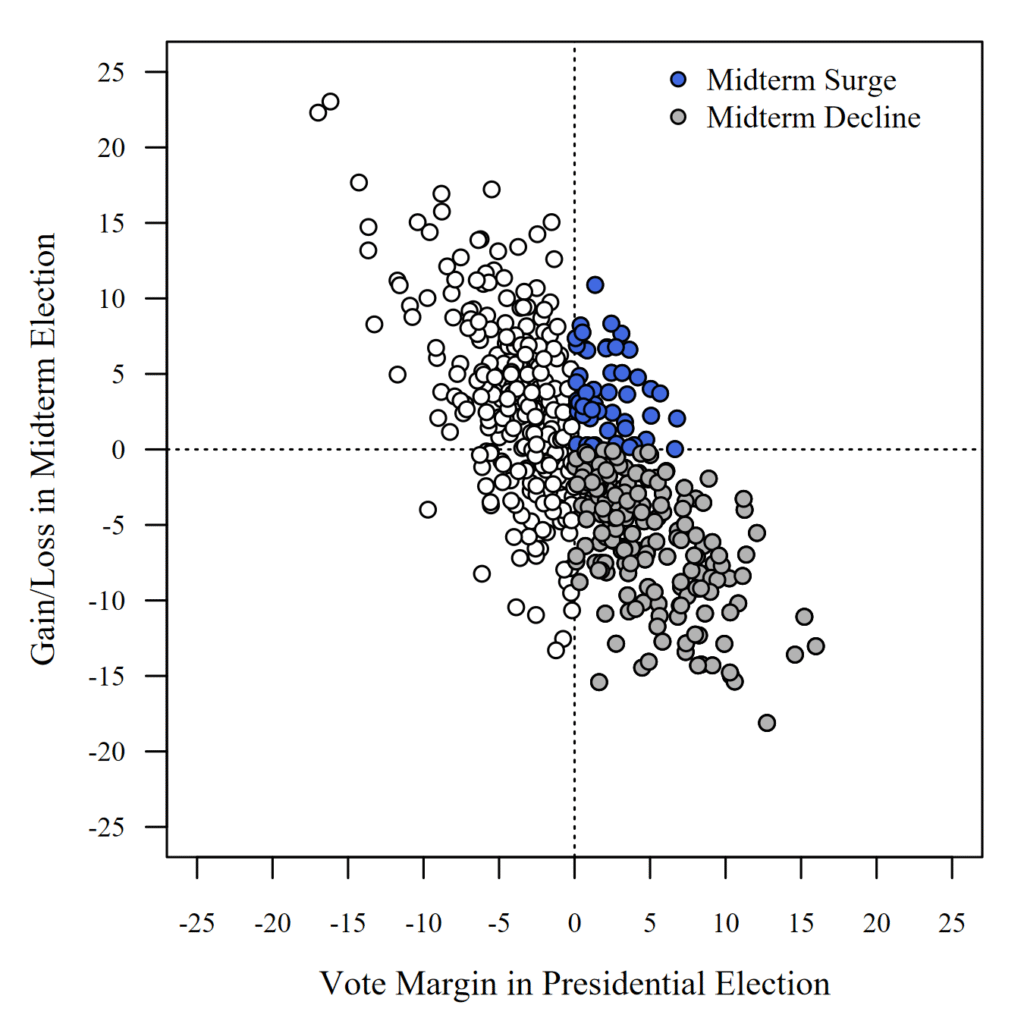
The regression analysis yields a specific prediction: every percentage point advantage in the presidential election should correspond to a proportional decline in the midterm election. If a party prevails by 6 percent points in the presidential election, the model predicts a 6 percent point decline in the midterm. This inverse relationship is the same regardless of the standard deviation of the vote share.

Based on this model, the party that win the presidential election can be expected to lose vote share in 75% of subsequent midterm elections. (The median of winning vote shares is the 75% percentile of expected vote shares.)

The mean margin of victory will be 3.99 percentage points (more generally, 0.798 x SD), a bit larger than the 3.37 median margin of victory because the margins of victory are positive skewed. The party that wins the presidential election experiences a mean decline of 3.99 percentage points in this vote share (median decline of 3.86 percentage points).

The midterm surge and decline phenomenon may tell us more about statistical properties of electoral competition than about voter psychology or political dynamics. While the pattern appears consistently in American elections, this consistency might reflect the natural consequence of competitive two-party systems rather than meaningful shifts in public opinion or partisan enthusiasm.

This perspective doesn’t diminish the importance of electoral research, but it does suggest that scholars should consider whether their sophisticated behavioral theories explain outcomes any better than simpler statistical models. As we continue to study American electoral patterns, distinguishing between genuine political phenomena and statistical artifacts becomes increasingly important for understanding democratic competition.

Suggestions for Further Research

I would challenge students of American politics to demonstrate that observed patterns of midterm surge and decline are significantly different than the pattern generated following the assumption that two-vote shares are normally distributed around a mean of 50 percentage points. This model yields expected midterm decline of .798 x SD percentage points. I suspect the supposed Midterm Decline pattern is regression to the mean rather than any systematic political phenomena, but those suspicions await further research.

This perspective doesn’t diminish the importance of electoral research, but it does suggest that scholars should consider whether their sophisticated behavioral theories explain outcomes any better than simpler statistical models. As we continue to study American electoral patterns, distinguishing between genuine political phenomena and statistical artifacts becomes increasingly important for understanding democratic competition.